圆

圆的定义

定义 1（动态）

在平面内把线段 $OP$ 绕着端点 $O$ 旋转一周，另端点 $P$ 运动所形成的图形叫做圆，其中，点 $O$ 叫做圆心，线段 $OP$ 叫做半径。

• 圆心 $\to$ 位置（定点）；
• 半径 $\to$ 大小（定长）。

定义 2（静态）

圆心为 $O$,半径为 $r$ 的圆可以看成是所有到定点 $O$ 的距离等于定长 $r$ 的点组成的图形。

圆的表示方法

以点 $O$ 为圆心的圆，记作“$\odot O$”，读作“圆 $O$”。

• 圆心相同 且 半径相等 的圆叫做 同圆；
• 能够重合^[1]的两个圆叫做 等圆；
• 圆心相同，半径不相等 的两个圆叫做 同心圆。

弦

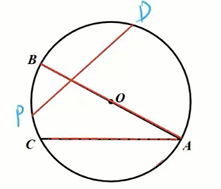
弦：连接 圆上 任意两点的线段叫做弦，如弦 $AC$。
直径：经过圆心的弦叫做直径，如直径 $AB$。

• 圆中有无数条弦，其中 直径是圆中最长的弦；
• 圆的对称轴是直径所在的直线。

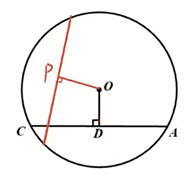
弦心距

圆心到一条弦的距离，叫做这条弦的弦心距，如 $OD$。

弧

弧：圆上任意两点间的部分叫做圆弧，简称弧。以 $A$，$C$ 为端点的弧记作 $\text{overgroup}AC$，读作“圆弧 $AC$”或“弧 $AC$”。
半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。
优弧：大于半圆的弧叫做优弧（用三个点表示，如图中的 $\text{overgroup}ABC$）。
劣弧：小于半圆的弧叫做劣弧（如图中的 $\text{overgroup}BC$）。
等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。

点与圆的位置关系

设 $\odot O$ 的半径为 $r$，点到圆心的距离为 $d$，则有：

点与圆的位置关系	$d$ 与 $r$ 的大小关系
点在圆内	$d<r$
点在圆上	$d=r$
点在圆外	$d>r$

垂径定理

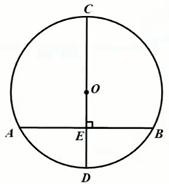
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

知二推三，条件和结论只要知道任意两个，就能推出另外 3 个。

• 条件
  • 直径（过圆心）$\to$ 圆心
  • 垂直于弦（非直径）$\to$ 垂足
• 结论
  • 平分弦 $\to$ 弦中点
  • 平分优弧 $\to$ 优弧中点
  • 平分劣弧 $\to$ 劣弧中点

见弦思垂 + 勾股定理。

几何语言

$\because$ $CD$ 是 $\odot O$ 的直径，$AB$ 为弦，$CD\perp AB$
$\therefore$ $AE=BE$，$\text{overgroup}AD=\text{overgroup}BD$，$\text{overgroup}AC=\text{overgroup}BC$

圆心角

定义

顶点在 圆心 的角叫做圆心角。

定理 1

在同圆或等圆中，相等的 圆心角 所对的 弧 相等，所对的 弦 也相等。

定理 2:

在同圆或等圆中，如果两条 弧 相等，那么它们所对的 圆心角 相等，所对的 弦 相等。

定理 3:

在同圆或等圆中，如果两条 弦 相等，那么它们所对的 圆心角 相等，所对的 优弧 和 劣弧 分别相等。

总结

在同圆或等圆中，等圆心角 $⟺$ 等弧 $⟺$ 等弦，这三个条件“知一推二”。

易错点

前提是 在同圆或等圆中。

圆周角

如图，像 $\angle ACB$，$\angle ADB$，$\angle AEB$ 这样的 顶点在圆上，并且 两边都与圆相交 的角叫做圆周角。

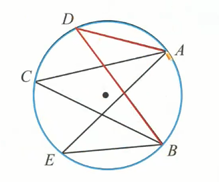
圆周角定理

一条弧 所对的 圆周角 等于它所对的 圆心角 的 一半。

圆周角定理推论 1

同弧或等弧所对 的圆周角相等。

圆周角定理推论 2

半圆（或直径）所对的圆周角是直角，$90°$ 的圆周角所对的弦是直径。
如图：$\angle AMB=\angle ANB=90°$

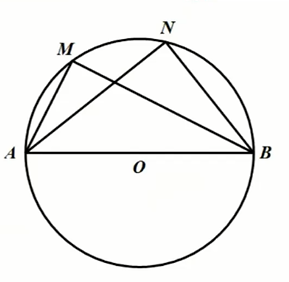
圆中辅助线做法

• 连半径
• 见弦思垂
• 见直径，想 $90°$

圆周角定理推论 3

圆内接四边形的对角互补。
圆内接四边形的一个外角等于它的内对角。
如图：$\angle A+\angle C=180$，$\angle B+\angle D=180°$，$\angle D=\angle CBE$

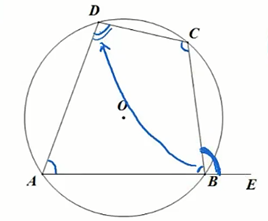
补充：圆内接四边形

四个顶点都在同一圆上的四边形叫做 圆内接四边形，这个圆叫做四边形的 外接圆。

贡献者

share121

页面历史

最后编辑于 2 天前

查看完整历史

2c1388f-refactor: 修改文档文件命名格式

ae6764b-docs: 修改头像链接

---

1. 圆心不同，半径相等。 ↩︎